16. ESTIMACION DEL ERROR DE UNA MEDIDA DIRECTA

La estimación del error de una medida tiene siempre una componente subjetiva. En efecto, nadie mejor que un observador experimentado para saber con buena aproximación cuál es el grado de confianza que le merece la medida que acaba de tomar. No existe un conjunto de reglas bien fundadas e inalterables que permitan determinar el error de una medida en todos los casos imaginables. Muchas veces es tan importante consignar cómo se ha obtenido un error como su propio valor.
Sin embargo, la aplicación de algunos métodos estadísticos permite objetivar en gran medida la estimación de errores aleatorios. La estadística permite obtener los parámetros de una población (en este caso el conjunto de todas las medidas que es posible tomar de una magnitud), a partir de una muestra (el número limitado de medidas que podemos tomar).

16.1 Mejor valor de un conjunto de medidas

Supongamos que medimos una magnitud un número n de veces. Debido a la existencia de errores aleatorios, las n medidas X1, X2,…., Xn serán en general diferentes.
El método más razonable para determinar el mejor valor de estas medidas es tomar el valor medio. En efecto, si los errores son debidos al azar, tan probable es que ocurran por defecto como por exceso, y al hacer la media se compensarán, por lo menos parcialmente. El valor medio se define por:
Una cantidad finita de números, es igual a la suma de todos ellos dividida entre el número de sumandos. Es uno de los principales estadísticos muéstrales. Expresada de forma más intuitiva, podemos decir que la media (aritmética) es la cantidad total de la variable distribuida a partes iguales entre cada observación, esto también es llamado promedio

y este es el valor que deberá darse como resultado de las medidas.

16.2 Dispersión y error. Desviación estándar
Evidentemente, el error de la medida debe estar relacionado con la dispersión de los valores; es decir, si todos los valores obtenidos en la medición son muy parecidos, es lógico pensar que el error es pequeño, mientras que si son muy diferentes, el error debe ser mayor.

Adoptando un criterio pesimista, podría decirse que el error es la semi diferencia entre el valor máximo y el mínimo. Por ejemplo, en una serie de medidas de una magnitud es más apropiado tomar como error la desviación media, es decir, el valor medio de la diferencia de los datos respecto al valor central. Sin embargo, como los datos difieren tanto por defecto como por exceso del valor medio, tal desviación se aproximaría a cero. Para evitarlo suele tomarse, no el valor medio de las desviaciones, sino el valor medio de las desviaciones al cuadrado. De esta forma todos los sumandos son positivos. Para que la unidad de este número sea homogénea con la de los datos, se extrae la raíz cuadrada. El valor resultante se llama desviación típica o desviación estándar del conjunto de datos.

16.3 Significado de la desviación estándar. La distribución normal

Los valores de la desviación estándar que hemos calculado son realmente estimadores de este parámetro. El conjunto de las medidas de una magnitud, siempre que exista un error accidental, pueden caracterizarse por medio de una distribución estadística. Cuando el error es debido a un gran número de pequeñas causas independientes, la distribución se aproxima a la llamada distribución normal.

La forma de representar en estadística una distribución es representando en abscisas el conjunto de valores que pueden obtenerse en una medida y en ordenadas la probabilidad de obtenerlos. En el caso de que la magnitud medida varíe de forma continua, en ordenadas se representa la probabilidad por unidad de intervalo de la magnitud medida.

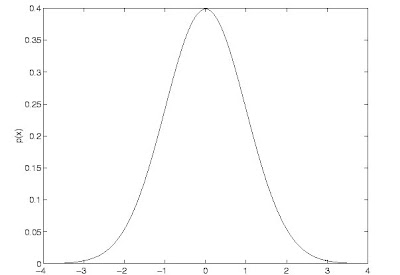Figura: Función de densidad de una distribución normal de media 0 y desviación estándar 1

La función de densidad de la distribución normal tiene el aspecto reflejado en la figura. Recibe también el nombre de campana de Gauss debido a su forma. Está caracterizada por dos parámetros: media y desviación estándar. La media es el valor que con mayor probabilidad aparecerá en una medida. La desviación estándar refleja lo abierta o cerrada que es la campana de Gauss correspondiente. Una distribución muy cerrada se corresponde con una serie de medidas muy poco dispersas, y por tanto con poco error. Por el contrario si la distribución es abierta, la desviación estándar es grande. Porque La desviación estándar de un conjunto de datos es una medida de cuánto se desvían los datos de su media.

Una de las propiedades de la distribución normal es que la probabilidad que encierra en el intervalo (m – σ, m + σ) es del 68.3 % aproximadamente. Es decir, es de esperar que el 68.3 % de las medidas de una magnitud estén comprendidas en ese intervalo. Dicho de otra forma, si medimos una magnitud un número grande de veces, el 68.3 % de los valores obtenidos estarán comprendidos en el entorno de una desviación estándar en torno a la media. La probabilidad se amplía al 95.4 % y al 99.7 % si consideramos los intervalos (m – 2σ, m + σ) y (m – 3σ, m + 3σ) respectivamente.

la distribución normal se debe a dos razones fundamentalmente:
- Su función de densidad es simétrica y con forma de campana, lo que favorece su aplicación como modelo a gran número de variables estadísticas.- Es, además, límite de otras distribuciones y aparece relacionada con multitud de resultados ligados a la teoría de las probabilidades gracias a sus propiedades matemáticas
El error expresado por la desviación estándar tiene por tanto un significado probabilística: hay una probabilidad del 68% de que una medida esté en el entorno de una desviación estándar alrededor de la media.

La distribución normal aparece con frecuencia en las medidas de magnitudes, pero no siempre. La distribución de una serie de medidas se aproxima a una normal siempre y cuando la fuente de error sea la superposición de muchas pequeñas causas independientes. Si hay una o varias causas de error predominantes o si las causas de error no son independientes, se dice que las medidas presentan un sesgo, y la distribución puede muy bien ser otra. Es muy frecuente encontrar distribuciones de medidas no simétricas, con dos o más máximos, etc.
Conviene insistir finalmente en que no es posible determinar la media y la desviación estándar de una distribución, sino solamente estimarlas.

16.4 Medidas sin dispersión. Error de lectura o instrumental

En ocasiones la repetición de la medida de una magnitud conduce siempre al mismo valor. Como ejemplo, consideremos la medida de la longitud de un objeto con una regla graduada en milímetros. Si la medida se realiza con cierta atención, todas las medidas del objeto proporcionan el mismo valor. Es evidente que en este caso la teoría de desviación estándar no aplica, porque al ser nula la dispersión, la desviación estándar resulta igual a cero. En estos casos, la fuente de error no está en la superposición de muchas causas aleatorias, sino en la sensibilidad del aparato de medida.

En efecto, el hecho de que todas las medidas sean iguales no indica en general que no haya error accidental, sino que éste es demasiado pequeño para quedar reflejado en el aparato. En el ejemplo anterior, si el error accidental de las medidas es del orden de 0,001 mm es evidente que la regla no podrá apreciarlo, resultando todas las medidas iguales. En estos casos es necesario estimar el error debido a la sensibilidad finita del aparato de medida.
Cuando se habla de lectura de un instrumento de medida indicador, se quiere significar la referencia de la posición relativa del índice y de la graduación, en esta apreciaciones se comete un error de lectura debido a las siguientes causas:

* Error de paralaje: este tipo de error resulta cuando la visual del operador no se encuentra perpendicular a la aguja del instrumento, sino más bien se encuentra ubicado en un cierto ángulo del mismo.

*Error debido al límite del poder separador del ojo humano : Se sabe que en condiciones normales de visibilidad la distancia angular mínima necesaria para observar dos puntos A y B separados según la figura, es de 2 minutos. En general, las escalas son, leídas desde una distancia media de aproximadamente 250 mm y esto muchas veces conlleva a errores de lectura por mucha distancia entre el instrumento y el observador.

*Error de estimación : se comete al leer valor de la desviación encontrándose la aguja entre dos divisiones sucesivas de la escala; en este caso existe cierta incertidumbre en la apreciación de la posición exacta de la aguja sobre la escala, incertidumbre que no se hace leer indistintamente mayor o menor que el verdadero y en una cantidad representada por la menor fracción que puede apreciarse de la división considerada sobre la escala..

Se llama sensibilidad de un aparato a la mínima variación de la magnitud medida que es capaz de detectar. En los instrumentos analógicos coincide frecuentemente con la mínima división de la escala. En el ejemplo anterior la sensibilidad de la regla es de 1 mm.
Suele llamarse apreciación al máximo error que puede cometerse debido a la sensibilidad del aparato. Generalmente se considera como la mitad de la sensibilidad. Esto puede comprenderse con un ejemplo. Supongamos un voltímetro de 0,1 V de sensibilidad, cuya aguja indica una tensión comprendida entre 2,1 V y 2,2 V, es decir, la aguja señala un punto intermedio entre las dos marcas o divisiones de la escala. Si el aparato está bien diseñado, una persona con apreciación visual media debe ser capaz de decidir si la aguja está más cerca de 2,1 V o de 2,2 V. Cometeremos el máximo error cuando la aguja se encuentre justamente en el centro de las dos divisiones. En tal caso el error de dar como lectura 2,1 V o 2,2 V es de 0,05 V, es decir la mitad de la sensibilidad.
En resumen, el error instrumental de una medida se expresa frecuentemente por:

donde s es la sensibilidad del aparato de medida.
Hemos visto que cuando el error instrumental es mucho mayor que el accidental, éste queda enmascarado por aquel. El efecto inverso es también posible. Por tanto, en los casos en que el error accidental de una medida sea mucho mayor que el instrumental, sólo consideraremos el error accidental.
16.5 Propagación de errores
Las operaciones matemáticas con números inciertos dan lugar a resultados también inciertos, y es importante poder estimar el error de los resultados a partir de los errores de los números con los que se opera.
Consideremos un ejemplo sencillo para ilustrar este tema. Supongamos que se mide el lado (x) de una parcela de terreno cuadrada, y a partir de esta medida quiere obtenerse su superficie (y). La medida del lado llevará aparejada un error, que puede ser de origen accidental, instrumental o combinación de ambos. Admitamos que el lado mide 8 m y que el error es de 1 m. El valor de la superficie es por tanto de 64 m2, y estamos interesados en estimar su error. En la figura de arriba se ha representado la superficie en función del lado. El error en la medida del lado puede interpretarse como el radio de un entorno alrededor del valor nominal, en cuyo interior estará el valor del lado con una determinada probabilidad. Si proyectamos este entorno sobre la curva obtendremos otro entorno en el eje de ordenadas que representa el error de la superficie. Inspeccionando la figura llegamos a la conclusión de que el error de la superficie es de algo más de 15 m2. En una medida de precisión normal, el error es lo suficientemente pequeño como para poder sustituir la curva por la recta tangente a la curva. La relación entre el error de y y el error de x será entonces la pendiente de la curva en el punto de interés. Es decir, la relación entre el error del lado y el error de la superficie es la derivada de la función:

En un caso más general tendremos dos o más variables en lugar de sólo una. Por ejemplo, si la parcela anterior es rectangular en vez de cuadrada, la superficie es función de dos variables: la base (x) y la altura (y). La medida de cada una de estas dos variables tendrá un cierto error, que se propagará al valor de la superficie: S=x.y. La contribución del error de cada lado al error de la superficie vendrá dado por una ecuación similar . Parece lógico pues que el error total de la función S sea la suma de las contribuciones de cada una de las variables
Es importante tener presente que esta expresión es válida sólo en los siguientes supuestos:
El error de cada variable es mucho menor que la propia variable.
Las variables son independientes en el sentido estadístico del término. Quiere esto decir que el valor de una de ellas no afecta en absoluto al valor de la otra. Por ejemplo, la estatura de una persona y su peso no son variables independientes. Si medimos el peso y la estatura de un gran número de personas llegaremos a la conclusión de que generalmente las personas más altas pesan también más.

16.6 Ajuste por mínimos cuadrados
Es una técnica de optimización matemática que, dada una serie de mediciones, intenta encontrar una función que se aproxime a los datos (un "mejor ajuste"). Intenta minimizar la suma de cuadrados de las diferencias ordenadas (llamadas residuos) entre los puntos generados por la función y los correspondientes en los datos. Específicamente, se llama mínimos cuadrados promedio (LMS) cuando el número de datos medidos es 1 y se usa el método de descenso por gradiente para minimizar el residuo cuadrado. Se sabe que LMS minimiza el residuo cuadrado esperado, con el mínimo de operaciones (por iteración). Pero requiere un gran número de iteraciones para converger.
Un requisito implícito para que funcione el método de mínimos cuadrados es que los errores de cada medida estén distribuidos de forma aleatoria.
Hasta ahora nos hemos ocupado de la manera de obtener el mejor valor de una magnitud a partir de una o varias medidas. Un problema más general es determinar la relación funcional entre dos magnitudes x e y como resultado de experimentos.
Supongamos que por razones teóricas bien fundadas sabemos que entre x e y existe la relación lineal

y=ax+b

y deseamos determinar los parámetros a y b a partir de n medidas de x e y. a es la pendiente de la recta, es decir, la tangente del ángulo que forma con el eje de abscisas, y b la ordenada en el origen, es decir la altura a la que corta la recta al eje de ordenadas. Para concretar, supongamos que los valores que han resultado de un experimento son los siguientes:

Xi= 1 2 3 4 5 6
Yi= 1.5 2.5 4.0 3.6 5.9 6.1

Ante un problema de este tipo, lo primero que conviene hacer es representar gráficamente los resultados para observar si los valores medidos se aproximan a una recta o no. En la figura 3 se han representado las medidas anteriores.

A la vista del gráfico parece claro que las dos variables siguen una relación lineal. La recta que parece representar mejor la relación se ha dibujado ``a ojo''. Es importante darse cuenta de que los seis puntos dibujados no pasan todos por la misma recta. Esto es debido a los errores de las medidas, por lo que los puntos se distribuyen de forma más o menos aleatoria en torno a esa recta. A pesar de ello es claramente visible la tendencia lineal de los puntos.
Para determinar la recta que mejor se adapta a los puntos se emplea el llamado método de los mínimos cuadrados. Para un valor de x determinado, la recta de ajuste proporciona un valor diferente de y del medido en el experimento. Esta diferencia será positiva para algunos puntos y negativa para otros, puesto que los puntos se disponen alrededor de la recta. Por este motivo, la suma de estas diferencias para todos los puntos es poco significativa (las diferencias negativas se compensan con las positivas).
Por ello, para medir la discrepancia entre la recta y los puntos, se emplea la suma de los cuadrados de las diferencias, con los que nos aseguramos de que todos los términos son positivos. Esta suma tiene la forma: